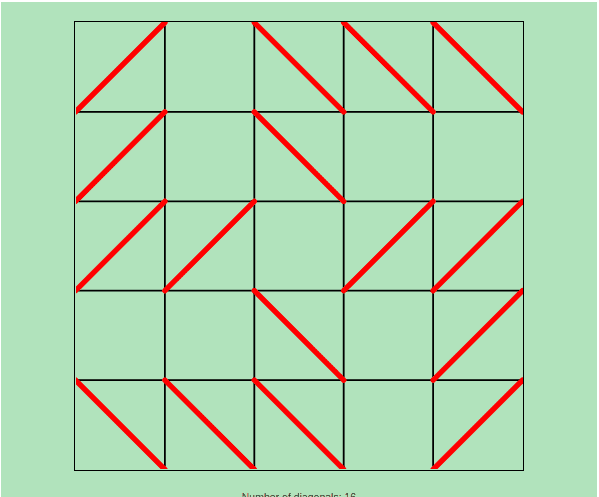
Solving N Diagonal Problem
Introduction
I took the What is a proof course on Coursera and found it very useful. The course provides useful knowledge about mathematical proofs. I found the course very useful and interesting. In this article I will describe one of the problems that were given to the students to solve.
In the N Diagonal problem, we have a board containing NxN squares. Each square can have 2 diagonals, but the diagonals of neighboring squares should not intersect. A square can have three possible states. Either empty, a left diagonal or a right diagonal. We need to find out if it is possible to have X number of diagonals.
Solution Overview
We have to go one step at a time, from the bottom left square and from left to right. A square can have 3 possible values. 0, 1 and 2. 0 means empty, 1 means diagonal is from right to left. 2 means diagonal is from left to right.
We can use a list to store the square values in Python. Python does not have built in support for arrays, so we can use a list instead.
First we need to find all possible values that a square can have. Since each square has three possible values, there are many possible combinations of values of a squares neighbors.
We can instead check if there is some combination of neighbor values which makes it impossible for the square to have a value of 1. Similarly we need to check if there is some combination of neighbor values which makes it impossible for the square to have a value of 2.
A square cannot have a value of 1 if the left square has a value of 2 or bottom square has a value of 2 or bottom right square has a value of 1.
A square cannot have a value of 2 if the left square has a value of 1 or bottom square has a value of 1 or bottom left square has a value of 2.
Pseudo Code
Here is the pseudo code:
function SolveNDiagonal(n, diag_count, arr, index):
if sum of 1s and 2s in list is more than N, then
print list
exit
For each x in arr starting from index upto NxN
values = GetPossibleValuesOfSquareAtX(n, arr, x)
For each val in values,
if val is more than 0, then
SolveNDiagonal(n, diag_count, arr, index+1)
The function is called as follows:
SolveNDiagonal(n, diag_count, arr, 0)Where n=5, diag_count=16, arr is a Python list initialized with 0s. The last parameter is the starting index, which is 0.
Source code in Python
# Main function
# n is the number of rows or cols in the board
# diag_count is the required number of diagonals
# arr is a list of size NxN
# index is the starting position
# The function prints state of all squares on the board
# Such that the board has diag_count number of diagonals
def solve_n_diagonal(n, diag_count, arr, index):
if (arr.count(1) + arr.count(2)) == diag_count:
print("Solved for n = " + str(n) +
" and diagonal count = " + str(diag_count))
print(arr)
exit()
for x in range(index, n*n):
values = get_element_values(n, arr, x)
for val in values:
arr[x] = val
if val > 0:
solve_n_diagonal(n, diag_count, arr, x+1)
# The values of neighboring squares
# We are only concerned with the values of squares on the
# left, bottom, bottom right and bottom left
def get_neighbor_values(n, arr, x):
neighbor_values = {"left": -1, "bottom_right": -1, "bottom_left": -1,
"bottom": -1}
if x % n != 0:
neighbor_values["left"] = arr[x-1]
if x >= n and (x % n != n -1):
neighbor_values["bottom_right"] = arr[x-(n-1)]
if x >= n and (x % n != 0):
neighbor_values["bottom_left"] = arr[x-(n+1)]
if x >= n:
neighbor_values["bottom"] = arr[x-n]
return neighbor_values
# Get the possible values that the square at position x can have
# The possible values are returned in a list
def get_element_values(n, arr, x):
neighbor_values = get_neighbor_values(n, arr, x)
values = list()
is_one_valid = True
is_two_valid = True
if (neighbor_values["left"] == 2 or neighbor_values["bottom"] == 2
or neighbor_values["bottom_right"] == 1):
is_one_valid = False
if (neighbor_values["left"] == 1 or neighbor_values["bottom"] == 1
or neighbor_values["bottom_left"] == 2):
is_two_valid = False
if is_one_valid:
values.append(1)
if is_two_valid:
values.append(2)
values.append(0)
return values
# Initialize a list of size n*n with 0s
def initialize_array(n):
arr = list()
for x in range(n*n):
arr.append(-1)
return arr
# The number of rows or cols in the board
n = 5
# The required number of diagonals
diag_count = 16
# The list is initialized
arr = initialize_array(n)
# The main function is called
solve_n_diagonal(n, diag_count, arr, 0)The above code prints the state of each square on a board, such that a square is either empty or it has a diagonal which does not intersect with the diagonals of its neighboring squares.